Research

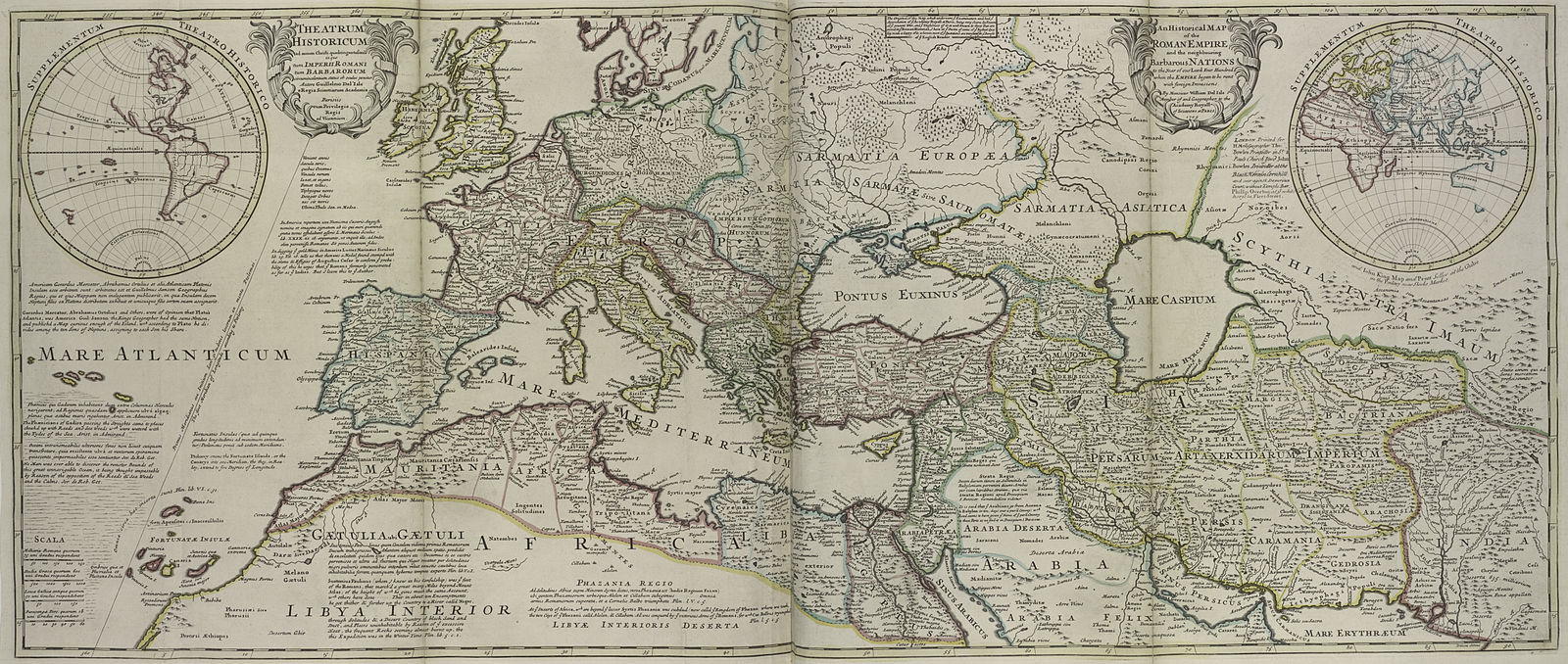From The Lionel Pincus and Princess Firyal Map Division.

A collaborative project in the overarching research topic "Geo meets Data Science and Fusion".

The project's main objective is the time series analysis of historical maps. To this end, a few processes will be selected as examples and examined in more detail in a dedicated work package. First, the temporal evolution of land cover or land use is analysed using classification approaches based on artificial intelligence (AI). Second, statistical modelling approaches are considered to gain insights into the development over time in different areas, e.g., urbanisation (How does the settlement area increase over time? Which factors influence urbanisation? To which extent can urbanisation be forecasted if the process will continue as before?), structural changes in agriculture (Are there patterns in the change of agricultural use, e.g. in the ratio of arable land to pasture land or land not used for agriculture?), temporal change in forest cover (How is the forested area changing? Where is forest damage likely to occur in future?), coast (How has the coastline or the structure of land use near the coast changed during the observation period? Temporal development of floodplains e.g. along river courses that have been regulated in the course of the observation period?).

The project deals with an important, fundamental problem of spatial and spatiotemporal statistics – the full estimation of the underlying spatial dependence structure. For these models, the focus has so far been on processes showing a dependence in the conditional means. That is, the mean of a realization of the random process at a particular measurement point depends on the adjacent observations. This finding goes back to Tobler’s first law of Geography. The surrounding observations are defined on the basis of their geographical proximity, although this does not necessarily lead to a dependence of the observations of the random variables, i.e. the covariances.

Various application examples will be used to demonstrate how the estimated parameters can be interpreted. Here, the focus will be on natural processes in the environment, such as air pollution or particulate matter. Using freely available sensor data, the results can be used, for example, to obtain local predictions of fine dust pollution in an urban area, which can then be used for optimal routing with respect to air quality.

Recently, various research has analysed the impact of agriculture and livestock farming on air quality that link emissions to concentrations. Using statistical modelling and machine learning, our project intends to evaluate the impact of agriculture on PM2.5 on a local scale. It allows the decision-maker to understand the local impact on the air quality of a certain local reduction of emissions. Hence, it can help them in localising and prioritising the interventions.

The project is carried out by an international group of researchers from the Universities of Bergamo, Turin, Milan-Bicocca and Hannover. Link to the official project website (in Italian): here

The project aims to develop new models in spatial statistics, which deal with the analysis of random processes in space. Such processes are essential in empirical research and particularly in econometrics. For instance, spatial statistics covers the analysis of processes on the surface of the Earth or the atmosphere, like air pollutants and particulate matters, regional prices for building land, or the population in municipalities. Observations close together in space are generally more similar than observations that are more distant in space; e.g., if the prices for building land are high in one municipality, then one might expect high prices in the neighbouring municipalities. Spatial autoregressive processes can model this phenomenon.

Besides this spatial dependence of the observed values, an analogue dependence can be observed for the variation of the data and the conditional heteroscedasticity. This project should develop statistical models for data showing this behaviour. In addition, a multivariate spatial ARCH model should be introduced, such that several statistical variables can be modelled simultaneously, like several environmental pollutants and particulate matters.

The project aims to extend the current mathematical and statistical research on spatial clusters, also known as spatial structural breaks (for spatially independent processes, e.g., Kulldorf, Nagarwall (1995), Amin, Hendryx, Shull, Bohnert (2014); for spatially dependent processes, e.g., Otto, Schmid (2016), Garthoff, Otto (2016)), by the temporal surveillance of spatial clusters. In particular, the focus is on non-linear spatial models.